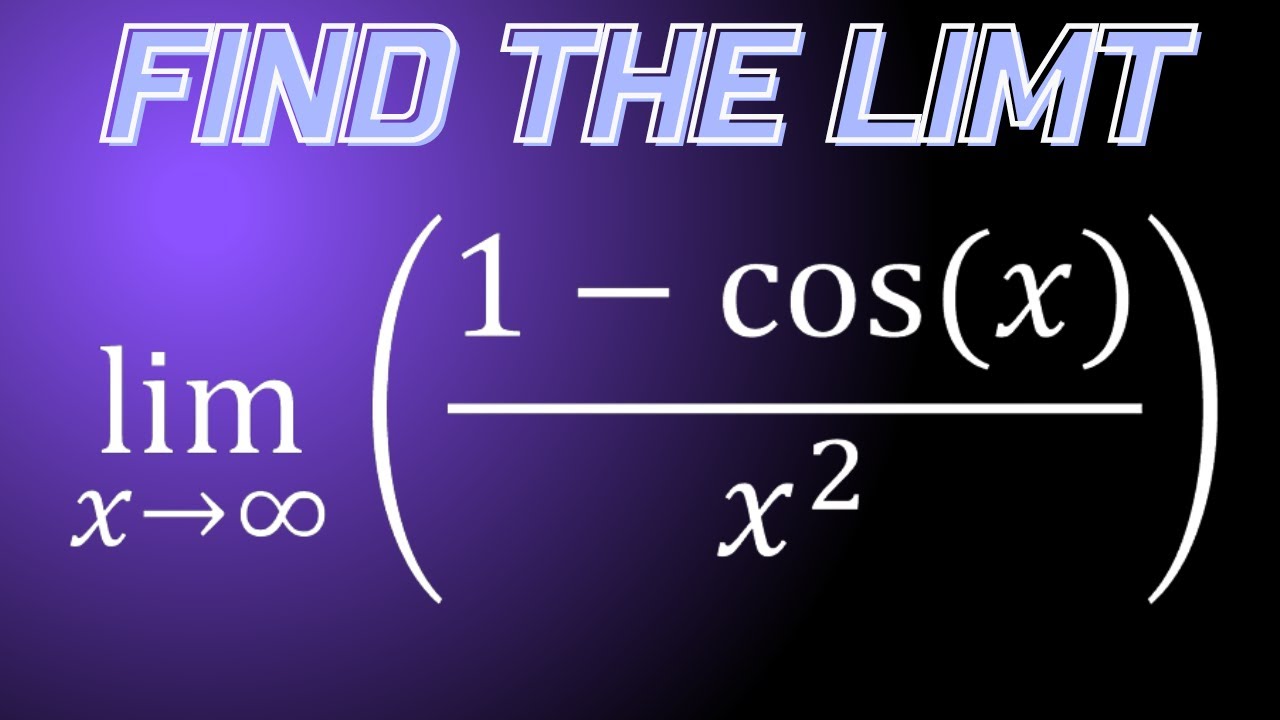Limit Of 1 Cosxx As X Approaches Infinity

This article discusses the limit of cos(x) as x approaches infinity. It provides educators with strategies for teaching this concept. We address common student misconceptions. We also suggest engaging activities.

Understanding the Limit Concept

The concept of a limit is fundamental in calculus. A limit describes the value that a function approaches. This is as the input (x) gets arbitrarily close to a certain value. This value can be a finite number or infinity. It is crucial to introduce this idea intuitively before diving into formal definitions. Examples using simpler functions like f(x) = 1/x as x approaches infinity are helpful.

Visual aids are essential. Use graphs to illustrate how the function behaves. Emphasize that the limit is not necessarily the value of the function *at* the point. Rather it is the value it is *approaching*. Consider functions with holes or asymptotes. This will solidify the understanding of limits.

The Oscillation of Cos(x)

The cosine function, cos(x), is a periodic function. It oscillates between -1 and 1. This oscillation continues indefinitely. This is as x increases without bound (approaches infinity). Unlike functions that converge to a single value, cos(x) never settles down.

Imagine a bouncing ball that never loses energy. It continues to bounce between two fixed heights. Similarly, cos(x) perpetually oscillates. It never approaches a single, specific value. Therefore, the limit does not exist.

Why the Limit Does Not Exist

For a limit to exist, the function must approach a single, unique value. This has to happen as x approaches infinity. The cos(x) function violates this requirement. It takes on infinitely many values between -1 and 1. It never settles on one particular value.

Consider two sequences of x values. One sequence makes cos(x) approach 1. Another sequence makes cos(x) approach -1. Since we get different limit values depending on the sequence, the overall limit does not exist. This highlights the formal definition of a limit.

Teaching Strategies

Start with the graphical representation of cos(x). Show students how the graph oscillates continuously. Emphasize that there is no convergence. Ask students to predict what happens to the value of cos(x) as x becomes very large. Guide them to realize that it just keeps oscillating.

Use dynamic geometry software. Allow students to manipulate the value of x. Observe the corresponding value of cos(x). This provides an interactive visual experience. It reinforces the concept of oscillation. You can use online graphing tools to demonstrate this.

Relate this to real-world scenarios. Consider periodic phenomena like sound waves or alternating current. While these have defined frequencies, they don't converge to a single "ultimate" value as time goes to infinity. Therefore, they illustrate similar oscillatory behavior.

Addressing Common Misconceptions

Some students may incorrectly assume the limit is zero. This is because they confuse cos(x) with functions that approach zero. Address this misconception directly. Emphasize that while the function oscillates, it never consistently gets closer to zero.

Another misconception is assuming the limit is undefined because it "goes up and down." Clarify that "undefined" has a specific mathematical meaning. The limit does not exist because it does not approach a single value. Not necessarily because there is some kind of mathematical impossibility.

Encourage students to clearly articulate their reasoning. Ask them *why* they think the limit exists or doesn't exist. This helps identify underlying misunderstandings. It allows you to provide targeted feedback. It is important to address these misconceptions head-on.

Engaging Activities

Conduct a class discussion. Ask students to brainstorm other functions that do not have limits at infinity. This encourages critical thinking. It reinforces the understanding of what constitutes a limit.

Have students create a visual representation of the concept. This could be a drawing, a diagram, or even a short animation. Visualizing the concept can help solidify their understanding. It also allows for different learning styles.

Assign a research project. Have students investigate the limits of other trigonometric functions. This promotes independent learning. It encourages them to apply the concepts learned in class.

Using Sequences to Understand the Limit

Introduce the idea of sequences. A sequence is a list of numbers. These numbers often follow a particular pattern. For instance, x_n = n generates the sequence 1, 2, 3, 4, ... .

Consider two sequences: x_n = 2πn and y_n = π + 2πn, where n is an integer. As n approaches infinity, both x_n and y_n also approach infinity. However, cos(x_n) = cos(2πn) = 1 for all n. And cos(y_n) = cos(π + 2πn) = -1 for all n.

This demonstrates that even though both sequences x_n and y_n approach infinity. The function values cos(x_n) and cos(y_n) approach different limits (1 and -1, respectively). Therefore, the limit of cos(x) as x approaches infinity does not exist.

Conclusion

Teaching the limit of cos(x) as x approaches infinity requires careful explanation. It also requires visual aids. It is important to address common misconceptions. By using engaging activities, educators can help students grasp this challenging concept. Understanding limits is crucial for further studies in calculus and related fields. It is an important building block for higher mathematics.