Imagine you have some pizzas. Let's say you have 5 whole pizzas and then 6/7 of another pizza. This means you have more than just whole pizzas; you have a part of a pizza too.
What are Fractions, Mixed Numbers, and Improper Fractions?
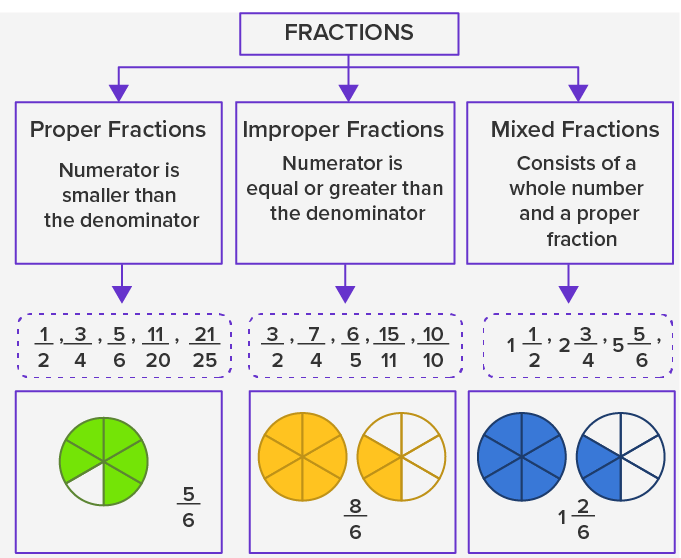
First, let's define some terms. A fraction is a way to represent a part of a whole. It has two parts: the numerator and the denominator. The numerator (top number) tells you how many parts you have. The denominator (bottom number) tells you how many parts make up the whole.
For example, in the fraction 1/2, the numerator is 1, and the denominator is 2. This means you have 1 part out of 2 needed to make a whole. Imagine cutting a pizza into two equal slices; 1/2 represents one of those slices.
A mixed number is a combination of a whole number and a fraction. It represents a quantity greater than one. For instance, 1 1/2 is a mixed number representing one whole and one-half. This means you have a full pizza, and half of another pizza.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. In other words, the top number is bigger than or equal to the bottom number. Examples of improper fractions are 7/2, 5/5, and 10/3. These fractions represent a quantity greater than or equal to one whole.
Understanding 5 6/7
The number 5 6/7 is a mixed number. It consists of a whole number (5) and a proper fraction (6/7). This signifies that you have five complete units (like pizzas) and six-sevenths of another unit. Let's see how to convert this into an improper fraction.
Converting a Mixed Number to an Improper Fraction
Now, let's learn how to convert a mixed number like 5 6/7 into an improper fraction. This is a crucial skill. There are only a couple of steps.
The first step is to multiply the whole number by the denominator of the fraction. In our example, we multiply 5 (the whole number) by 7 (the denominator). That is, 5 * 7 = 35.
The second step is to add the result from the previous step to the numerator of the fraction. In our case, we add 35 to 6 (the numerator). That is, 35 + 6 = 41.
The third step is to write the result from the previous step as the new numerator. The denominator stays the same. Therefore, our improper fraction is 41/7. This means the mixed number 5 6/7 is equivalent to the improper fraction 41/7. The denominator remains 7, because the parts are still divided into sevenths.
A Quick Recap of the Steps:
Step 1: Multiply the whole number by the denominator. 5 * 7 = 35 Step 2: Add the result to the numerator. 35 + 6 = 41 Step 3: Write the result as the new numerator, keeping the same denominator. 41/7
Why Does This Work?
Consider again the mixed number 5 6/7. The whole number 5 represents 5 complete units. If each of these units is divided into 7 parts (as indicated by the denominator), then 5 whole units contain 5 * 7 = 35 parts. We also have 6/7 of another unit, meaning we have an additional 6 parts. Therefore, in total, we have 35 + 6 = 41 parts, each of size 1/7. This gives us the improper fraction 41/7.
Think of it like this: if you have 5 whole pizzas and each pizza is cut into 7 slices, you have 35 slices. Then you have another pizza with 6 slices. In total, you have 41 slices, where each slice is 1/7 of a pizza. This is the fraction 41/7.
Another Example
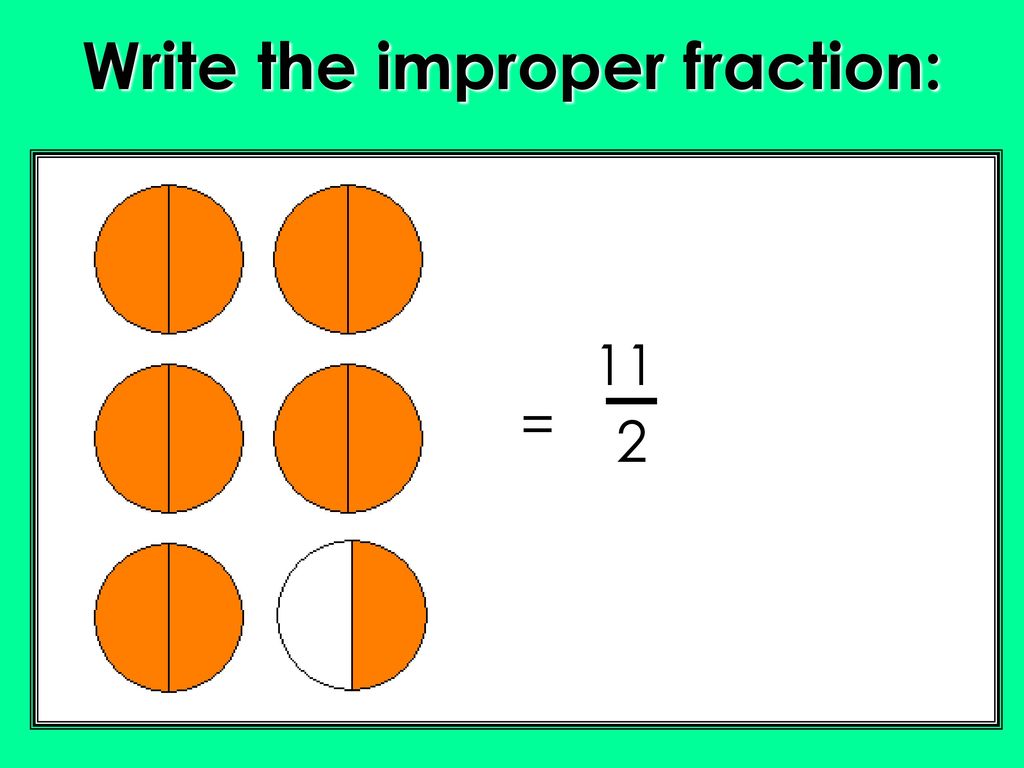
Let's convert 2 3/4 into an improper fraction. Step 1: Multiply the whole number by the denominator: 2 * 4 = 8 Step 2: Add the result to the numerator: 8 + 3 = 11 Step 3: Write the result as the new numerator, keeping the same denominator: 11/4
So, 2 3/4 is equal to 11/4. Imagine having two whole pies, and each pie is divided into 4 slices. You have 8 slices. You also have 3 slices from another pie. In total, you have 11 slices, and each slice is 1/4 of a pie. Thus, 11/4 represents having 11 quarter-pie slices.
Practice Makes Perfect
Converting mixed numbers to improper fractions is a fundamental skill in mathematics. Once you understand the logic behind the process, converting between these two forms of numbers becomes simple. Remember to practice these conversions regularly.
Try converting these mixed numbers to improper fractions on your own: 3 1/2, 4 2/5, 1 7/8. After some practice, you’ll find that working with fractions is no problem at all! Always remember what the numerator and the denominator represent.
Understanding fractions will give you a better understanding in topics such as algebra, trigonometry, and calculus. Mastering them now will help you later on.
Don't hesitate to search for more examples or consult your teacher or professor if you have more questions. Now you know all about how 5 6/7 can be converted into an improper fraction!