Let's explore how to express whole numbers as improper fractions.
Understanding Whole Numbers as Fractions
Any whole number can be represented as a fraction. The key is to understand what a fraction represents. A fraction shows a part of a whole, but it can also represent more than one whole.
Consider the whole number 4. We want to rewrite it as a fraction. We can write it as 4/1. The denominator, 1, indicates that we are considering one whole, and the numerator, 4, indicates that we have four of those wholes.
Here is a crucial point: Any whole number, 'n', can be expressed as n/1.
Teaching Tip: Visual Aids
Use visual aids to demonstrate this concept. Draw four circles, each representing one whole. Divide each circle into one part. Show students that they have four out of one part in each circle.
You can also use manipulatives like fraction bars. Show four whole fraction bars, and explain that each represents 1/1. Combining them gives you 4/1.
Improper Fractions Defined
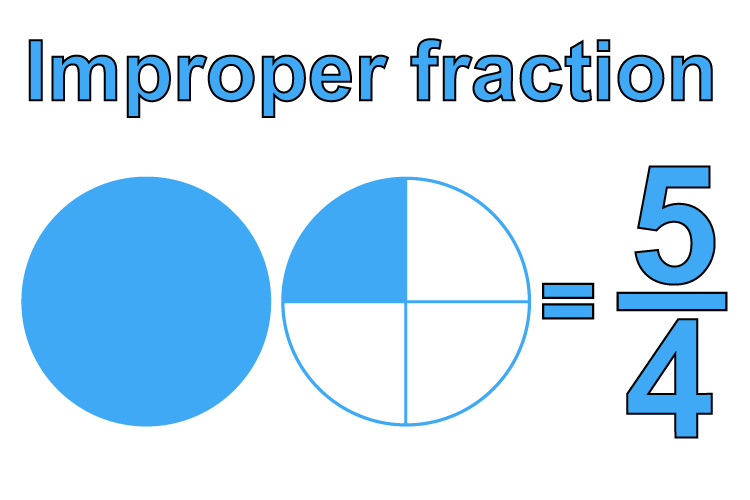
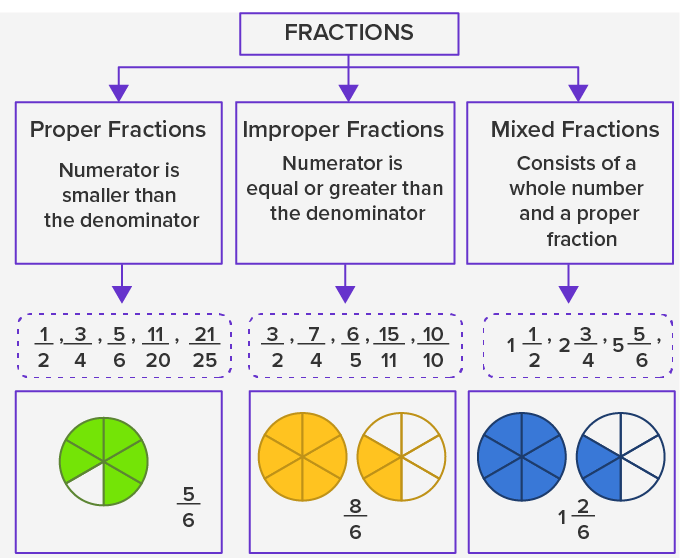
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 5/3 and 7/2 are improper fractions. The numerator is larger than the denominator in both examples.
When the numerator and denominator are equal (e.g., 3/3), the fraction equals one whole. In essence, improper fractions represent one or more whole units.
Think about a pizza cut into 8 slices. If you have 10 slices, you have more than one whole pizza. That can be represented as 10/8, which is an improper fraction. This translates to one whole pizza and two extra slices.
Teaching Tip: Real-World Examples
Use real-world examples like pizza or measuring cups. Relate the concept to things students already understand. Ask questions like: "If a recipe calls for 1/2 cup of flour, and you use three half-cups, how much flour did you use?" This leads to the improper fraction 3/2.
Expressing 4, 5, and 9 as Improper Fractions
Now, let's convert the whole numbers 4, 5, and 9 into improper fractions. Following the n/1 rule:
4 = 4/1
5 = 5/1
9 = 9/1
These are all improper fractions because the numerator is greater than the denominator (or equal to, in cases where the fraction represents one whole if simplified, which 4/1, 5/1, and 9/1 can be expressed as). In this case, it signifies that we have more than one whole. Each of these fractions represents multiple "wholes".
We could also express these whole numbers as improper fractions with different denominators. To do this, multiply both the numerator and denominator of the fraction (n/1) by the same number. For example:
4 = 4/1 = 4 x 2/1 x 2 = 8/2
5 = 5/1 = 5 x 3/1 x 3 = 15/3
9 = 9/1 = 9 x 4/1 x 4 = 36/4
These are also valid representations of the whole numbers as improper fractions.
Common Misconceptions
One common misconception is that improper fractions are "wrong" or "bad." Emphasize that they are simply another way to represent numbers, especially when dealing with quantities greater than one whole.
Another misconception is that the denominator always represents the total number of parts. Remind students that the denominator represents the size of each part, not necessarily the total count of all parts.
Students sometimes struggle with the concept of equivalent fractions. They might not understand that 4/1, 8/2 and 12/3 all represent the same quantity (the whole number 4). Spend time reinforcing the idea of equivalent fractions before introducing improper fractions.
Engaging Activities
Fraction Games: Play fraction games that involve converting between whole numbers, mixed numbers, and improper fractions. There are many online and board games available. For example, create a card game where students match a whole number with its improper fraction representation.
Cooking Activities: Baking or cooking provides a hands-on way to work with fractions. Let students measure ingredients and calculate quantities. For instance, double a recipe that calls for 1/4 cup of sugar. This requires working with improper fractions (2/4 = 1/2).
Story Problems: Create story problems that require students to use improper fractions to solve them. Example: "Sarah has 3 pizzas, each cut into 6 slices. How many slices does she have in total? Write this as an improper fraction."
By using visual aids, real-world examples, and engaging activities, you can help your students develop a strong understanding of how to represent whole numbers as improper fractions and overcome common misconceptions.