Converting decimals to fractions is a fundamental concept in mathematics. Students must grasp this skill. Understanding fractions and decimals is crucial for various mathematical operations.
Understanding 0.55
0.55 represents fifty-five hundredths. This is the starting point. Recognizing the place value is essential. This understanding sets the stage for conversion.
Converting to a Fraction
Write 0.55 as a fraction with a denominator of 100. It becomes 55/100. This step directly reflects the decimal's place value. Explain how hundredths translate directly to the denominator.
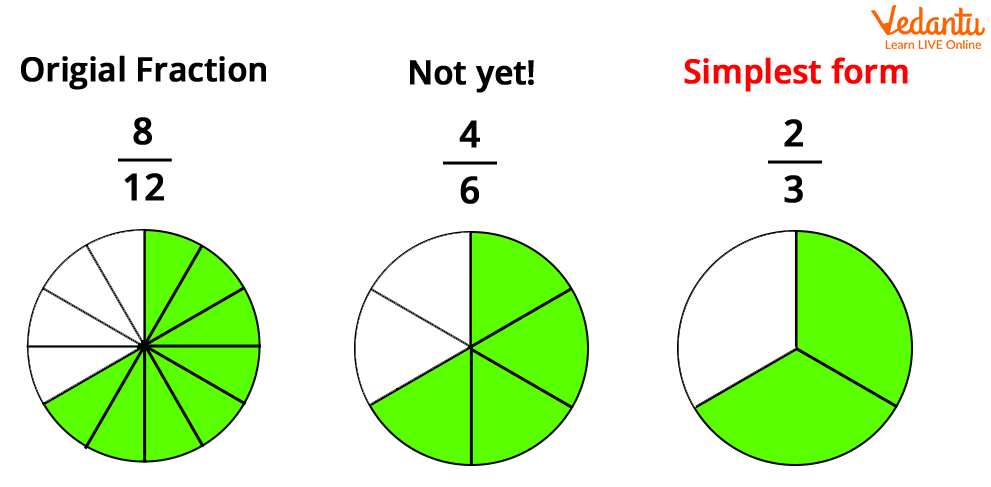
Simplifying Fractions
Simplifying fractions means finding the equivalent fraction. It must have the smallest possible numerator and denominator. This process makes fractions easier to understand and compare.
Finding the Greatest Common Factor (GCF)
The GCF is the largest number that divides both the numerator and denominator. For 55 and 100, the GCF is 5. Finding the GCF is crucial for simplifying to the simplest form.
Dividing by the GCF
Divide both the numerator and the denominator by the GCF. 55 ÷ 5 = 11 and 100 ÷ 5 = 20. This gives us the simplified fraction 11/20.
Therefore
0.55 as a fraction in simplest form is 11/20. This is the final answer. Make sure students understand that this is the most reduced form. Emphasize checking for further simplification.
Teaching Strategies for Educators
Engage students with visual aids. Use fraction bars or pie charts. These visual representations make the concept more concrete. Hands-on activities significantly improve comprehension.
Real-World Examples
Connect the concept to real-world scenarios. Use examples like sharing pizza or measuring ingredients. Relate the concept to their everyday lives. This will make learning more relevant.
Interactive Activities
Incorporate interactive games and activities. Online fraction games can be highly engaging. Activities like creating fraction flashcards can also be beneficial.
Step-by-Step Instructions
Provide clear, step-by-step instructions. Break down the process into manageable steps. This makes the process less overwhelming for students.
Common Misconceptions
Some students might struggle with identifying the place value. Others might forget to simplify the fraction. Addressing these common misconceptions is essential.
Incorrect Place Value
Students may confuse tenths and hundredths. Reinforce the place value system with visual aids. Emphasize the importance of accurate place value identification.
Forgetting to Simplify
Some students might convert the decimal to a fraction but forget to simplify it. Remind them to always check for further simplification. Emphasize that simplest form is the ultimate goal.
Incorrect GCF
Students might choose an incorrect GCF, leading to incomplete simplification. Provide practice in finding the GCF. Offer strategies for systematically identifying the GCF.
Engaging Activities
Use games and activities to make learning fun. This helps students retain information better. Engagement boosts understanding and reduces anxiety.
Fraction Flashcards
Create flashcards with decimals on one side and fractions on the other. Use them for quick quizzes or matching games. This reinforces the connection between decimals and fractions.
Online Games
Utilize online fraction games to provide interactive practice. Many websites offer engaging fraction games. These games make learning enjoyable and interactive.
Real-Life Problems
Present real-life problems involving decimals and fractions. For example, ask students to calculate discounts or share recipes. This demonstrates the practical application of the concept.
Assessment Strategies
Regular assessments help monitor student understanding. Use a variety of assessment methods. This ensures a comprehensive evaluation of their knowledge.
Quizzes
Administer short quizzes to assess understanding. These quizzes can identify areas where students need more support. Frequent quizzes help reinforce learning.
Worksheets
Provide worksheets with a variety of problems. Include problems that require both conversion and simplification. Worksheets offer structured practice.
Class Discussions
Encourage class discussions to promote deeper understanding. Ask students to explain their reasoning. This helps identify and address misconceptions.
Adapting for Different Learners
Adapt your teaching strategies to meet the needs of all learners. Provide additional support for struggling students. Challenge advanced students with more complex problems.
Scaffolding
Provide scaffolding for students who need extra support. Break down the steps into even smaller parts. Offer one-on-one assistance when needed.
Extension Activities
Challenge advanced students with extension activities. Ask them to convert more complex decimals to fractions. Encourage them to explore different simplification methods.
Importance of Practice
Consistent practice is key to mastering this skill. Provide ample opportunities for students to practice converting decimals to fractions. Regular practice builds confidence and fluency.
Homework Assignments
Assign regular homework assignments to reinforce learning. Ensure that assignments include a variety of problem types. This helps students practice and consolidate their knowledge.
Review Sessions
Conduct regular review sessions to reinforce key concepts. Review common mistakes and misconceptions. Review sessions help solidify understanding.
Final Thoughts
Converting decimals to fractions and simplifying them is a crucial skill. Employing effective teaching strategies, addressing misconceptions, and providing ample practice will help students master this concept. This knowledge will empower them in their future mathematical endeavors. This is a vital step in their mathematical journey.