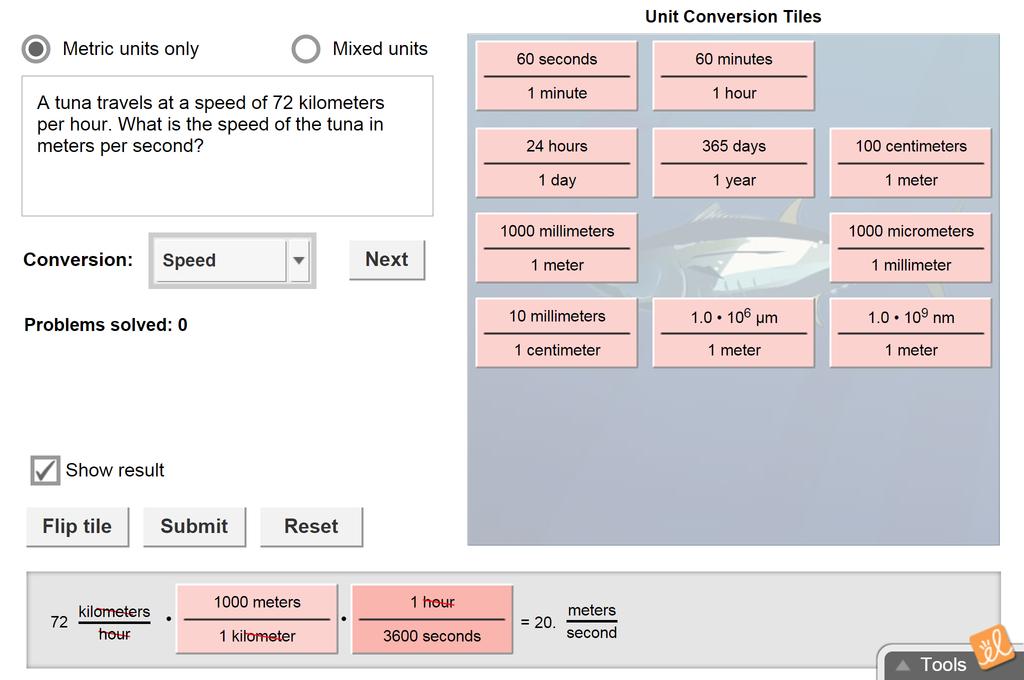
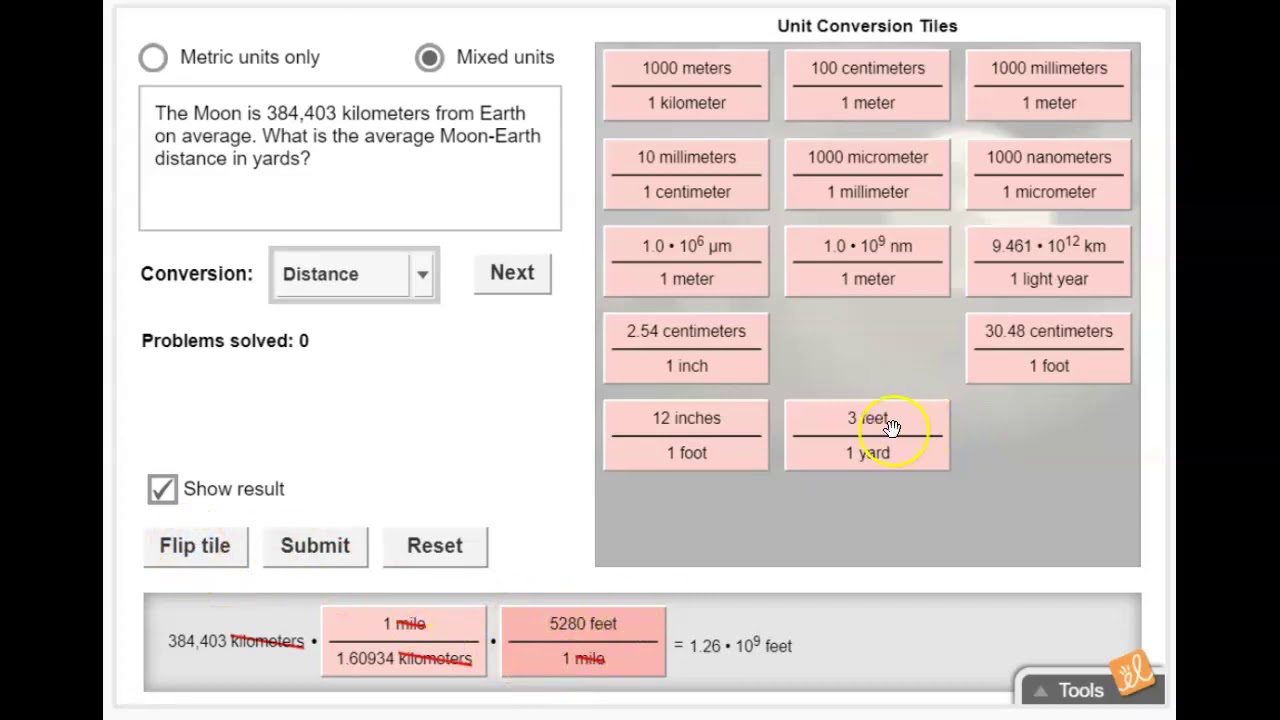
Unit conversions are a fundamental skill in science, engineering, and everyday life. They allow us to express measurements in different units while maintaining the same quantity. Understanding unit conversions is crucial for accurate calculations and clear communication.
What are Units?
A unit is a standard quantity used to express a measurement. We use units to quantify things like length, mass, time, and volume. For example, meters (m) are a unit of length, kilograms (kg) are a unit of mass, seconds (s) are a unit of time, and liters (L) are a unit of volume. We often need to change from one unit to another.
Different systems of measurement use different units. The two most common systems are the metric system and the imperial system. The metric system, also known as the International System of Units (SI), is used by most of the world. The imperial system, also known as the customary system, is used primarily in the United States.
Why Convert Units?
There are many reasons why we might need to convert units. Perhaps we are working with data from different sources that use different units. Or maybe we need to express a measurement in a more convenient unit for a particular application. Whatever the reason, knowing how to convert units is essential.
Consider a recipe that lists ingredients in cups and tablespoons. If we only have measuring tools in milliliters, we need to convert between these units. Another example is when traveling abroad. Knowing how to convert kilometers to miles can help us understand distances.
Conversion Factors
A conversion factor is a ratio that expresses the relationship between two different units. It is always equal to 1. We can use conversion factors to convert from one unit to another without changing the value of the quantity.
For example, we know that 1 meter is equal to 100 centimeters. Therefore, the conversion factor between meters and centimeters is 100 cm / 1 m (or 1 m / 100 cm). Both of these fractions are equal to 1, so multiplying by either one does not change the value of the quantity, only the units.
To use a conversion factor, we multiply the original quantity by the conversion factor, making sure that the original unit cancels out. For example, to convert 5 meters to centimeters, we would multiply 5 m by 100 cm / 1 m: 5 m * (100 cm / 1 m) = 500 cm. Notice that the "m" units cancel out, leaving us with centimeters.
Simple Unit Conversions
Let's look at some simple examples of unit conversions. Consider converting 3 kilometers (km) to meters (m). We know that 1 km = 1000 m. Therefore, the conversion factor is 1000 m / 1 km. To convert 3 km to meters, we multiply 3 km by 1000 m / 1 km: 3 km * (1000 m / 1 km) = 3000 m.
Another example is converting 10 kilograms (kg) to grams (g). We know that 1 kg = 1000 g. Therefore, the conversion factor is 1000 g / 1 kg. To convert 10 kg to grams, we multiply 10 kg by 1000 g / 1 kg: 10 kg * (1000 g / 1 kg) = 10000 g.
Now, let's convert 60 seconds (s) to minutes (min). We know that 60 s = 1 min. Therefore, the conversion factor is 1 min / 60 s. To convert 60 s to minutes, we multiply 60 s by 1 min / 60 s: 60 s * (1 min / 60 s) = 1 min.
Complex Unit Conversions
Some unit conversions are more complex and require multiple steps. For example, converting miles per hour (mph) to meters per second (m/s) requires converting miles to meters and hours to seconds. We know that 1 mile = 1609 meters and 1 hour = 3600 seconds. Therefore, we need two conversion factors: 1609 m / 1 mile and 1 hour / 3600 s.
To convert 60 mph to m/s, we multiply 60 mph by both conversion factors: 60 miles / 1 hour * (1609 m / 1 mile) * (1 hour / 3600 s) = 26.8 m/s. Notice how the miles and hours units cancel out, leaving us with meters per second.
Another example is converting square feet (ft2) to square meters (m2). We know that 1 foot = 0.3048 meters. However, since we are dealing with square units, we need to square the conversion factor: (1 foot)2 = (0.3048 meters)2, which means 1 ft2 = 0.0929 m2. To convert 100 ft2 to m2, we multiply 100 ft2 by 0.0929 m2 / 1 ft2: 100 ft2 * (0.0929 m2 / 1 ft2) = 9.29 m2.
The Unit Conversions 2 Gizmo
The Unit Conversions 2 Gizmo is an interactive online tool that helps students practice and master unit conversions. It provides a virtual environment where students can explore different units and conversion factors, allowing for a hands-on learning experience. Using interactive tools is important.
The Gizmo typically presents students with various conversion problems. It usually involves different types of units like length, area, volume, mass, and time. Using interactive tools is very helpful for learning.
While an "answer key" can provide quick solutions, focusing on understanding the process of unit conversion is crucial. The Gizmo is designed to help students develop this understanding by allowing them to experiment with different conversion factors and see the results firsthand. Understanding the underlying principles of conversions is what matters most.
Tips for Success with Unit Conversions
Always write down the units in every step of the calculation. This will help you keep track of the units and make sure they cancel out correctly. Using these concepts is very important.
Use conversion factors that are appropriate for the units you are converting. Double-check the conversion factors you use to ensure they are accurate. Reviewing basic concepts is really crucial.
Practice, practice, practice! The more you practice unit conversions, the better you will become at them. Practice makes perfect, as the saying goes. Consider doing many of the problems.
If you are unsure about a conversion, look it up online or in a textbook. There are many resources available to help you learn about unit conversions. There are a lot of great resources online.
Remember that unit conversions are a fundamental skill that will be useful in many areas of your life. Mastering this skill will make you a more confident and capable problem solver. Become great at problem-solving.