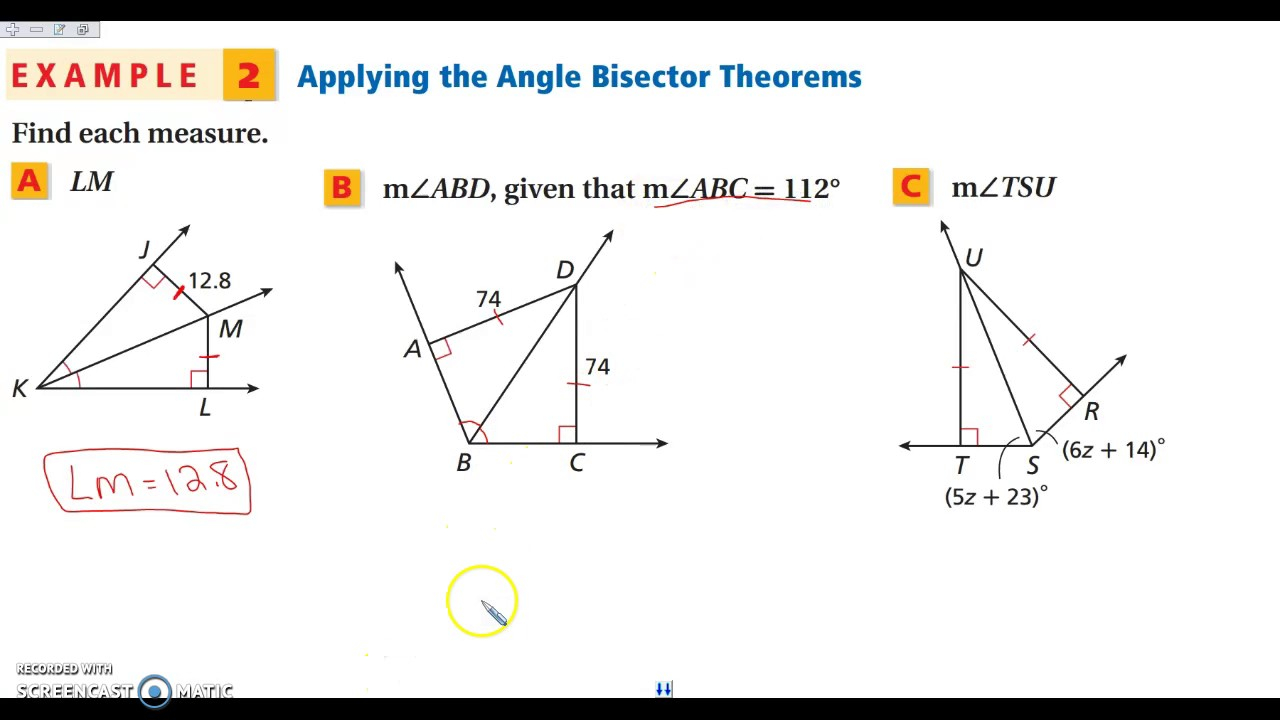
Let's explore perpendicular and angle bisectors.
Understanding Perpendicular Bisectors
A perpendicular bisector is key.
It's a line.
It intersects a segment at its midpoint.
It forms a right angle.
Explaining the Concept
Use visual aids.
Draw line segments.
Construct perpendicular bisectors.
Use a compass and straightedge.
Demonstrate the equal distances.
Any point on the bisector is equidistant from the endpoints.
Common Misconceptions
Students confuse it with just a bisector.
They forget the 90-degree angle.
Emphasize "perpendicular."
Clarify "bisector."
Address the "equal distance" property.
Making it Engaging
Use patty paper folding.
Students can fold the segment.
The crease is the perpendicular bisector.
Introduce real-world examples.
A bridge support is a good example.
It's perpendicular and bisects the weight distribution.
Use dynamic geometry software.
Students can manipulate the segment.
Observe the bisector's properties.
Understanding Angle Bisectors
An angle bisector divides an angle.
It creates two congruent angles.
Explaining the Concept
Draw angles.
Construct angle bisectors.
Again, use a compass and straightedge.
Show the congruent angles.
Introduce the Angle Bisector Theorem.
Points on the bisector are equidistant from the sides.
Common Misconceptions
Students assume equal segment lengths.
It's about equal angles, not necessarily segments.
The distance is measured perpendicularly.
Clarify this point.
Making it Engaging
Use paper folding again.
Fold the angle onto itself.
The crease is the angle bisector.
Relate it to symmetry.
An angle bisector creates symmetry.
Use a laser pointer and mirrors.
Show how the angle of incidence equals the angle of reflection.
Introduce navigation scenarios.
A boat changes course by bisecting an angle.
Connecting the Concepts
Both involve bisection.
One bisects a segment.
The other bisects an angle.
Both have "equal distance" properties.
Practical Applications
Construction uses these principles.
Architecture relies on symmetry and balance.
Navigation involves angles and distances.
Assessment Strategies
Include construction problems.
Students demonstrate their understanding.
Ask application questions.
Can they relate it to real-world scenarios?
Use multiple-choice questions.
Test their knowledge of definitions and theorems.
Error analysis is useful.
Give them a problem with an error.
Ask them to identify the mistake.
Tips for Educators
Be patient.
These concepts take time to grasp.
Provide ample practice opportunities.
Use a variety of teaching methods.
Visual, kinesthetic, and auditory learners all need catering to.
Encourage questions.
Address misconceptions promptly.
Relate it to other topics.
Connect it to triangle congruence or coordinate geometry.
Use technology wisely.
Dynamic geometry software can be a powerful tool.
Focus on the "why," not just the "how."
Help students understand the reasoning behind the theorems.
Emphasize the importance of accurate constructions.
Neatness matters!
Review prerequisite skills.
Students need a solid foundation in geometry.
Addressing Lesson 5.1 Specifically
Review the specific exercises.
Identify common areas of difficulty.
Provide targeted support.
Use the answer key as a guide.
Don't just give the answers.
Explain the reasoning behind them.
Use student work samples.
Show examples of correct and incorrect solutions.
Encourage peer teaching.
Students can learn from each other.
Create a supportive learning environment.
Students should feel comfortable asking questions.
Adapt the lesson to your students' needs.
Different classes learn at different paces.
Remember that understanding takes time.
By focusing on clear explanations, addressing misconceptions, and using engaging activities, you can help your students master the concepts of perpendicular and angle bisectors.