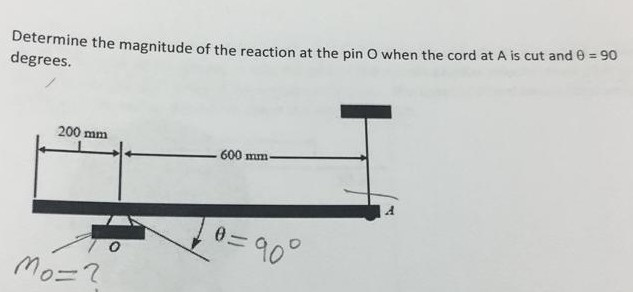
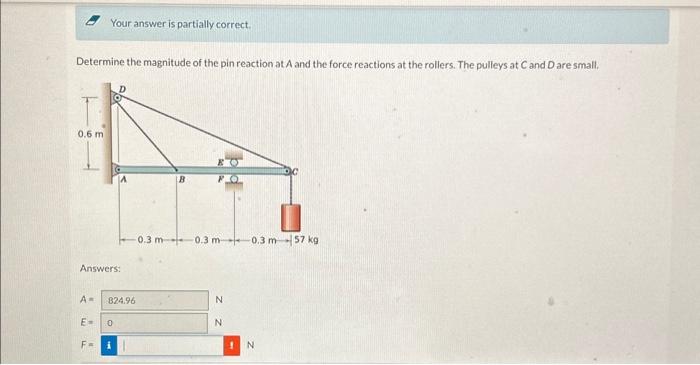
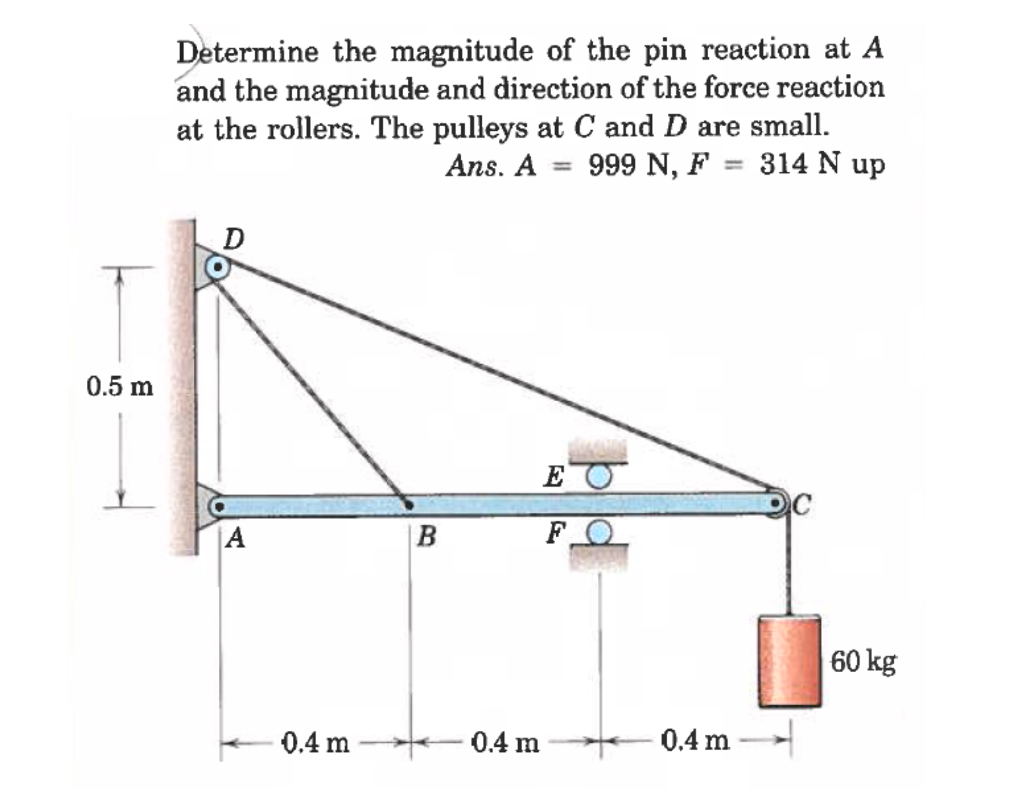
Let's talk about figuring out how much force is acting at a pin support, specifically at point A. It might sound complicated, but we can break it down.
What is a Pin Support?
Imagine a door hinged to a wall. The hinge allows the door to rotate freely. A pin support is like that hinge. It allows rotation but prevents movement in the horizontal and vertical directions.
Think of a seesaw. The pivot point in the middle is acting like a pin support. The seesaw can rotate but can't move up, down, left, or right (ideally!).
So, a pin support provides reactions. These are forces that resist any attempt to move the structure at that point. We want to find the magnitude, or size, of these reactions.
Understanding Reactions
Reactions are forces that a support exerts on a structure to keep it in equilibrium. Equilibrium means that the structure is not moving.
Imagine you're pushing against a wall. The wall is pushing back on you with an equal and opposite force. This is a reaction. If the wall didn't push back, you'd move through it!
For a pin support, there are two reaction forces: a horizontal reaction (often called Ax) and a vertical reaction (often called Ay). These reactions are what keep the structure from moving horizontally or vertically at the pin.
Key Concepts: Statics
To determine the magnitude of the reaction at pin A, we rely on the principles of statics. Statics deals with bodies at rest or in constant motion.
There are three main equations of equilibrium that we use. These equations ensure that the structure is not moving. They are fundamental to solving these types of problems.
These equations are:
- Sum of forces in the x-direction equals zero: ∑Fx = 0
- Sum of forces in the y-direction equals zero: ∑Fy = 0
- Sum of moments about any point equals zero: ∑M = 0
A moment is the turning effect of a force. It's calculated by multiplying the force by the perpendicular distance from the point of rotation to the line of action of the force.
The Steps to Solve for Reactions at Pin A
Here’s a step-by-step approach to finding the magnitude of the reactions at pin A. We will assume that we have a diagram of the structure with all the external forces acting on it.
1. Draw a Free Body Diagram (FBD)
A Free Body Diagram (FBD) is a simplified representation of the structure. It shows all the external forces acting on the structure, including the reactions at the supports.
Think of it like isolating the structure and showing all the pushes and pulls acting on it. Don't forget to include the weight of the structure if it's significant!
Replace the pin support at A with its horizontal (Ax) and vertical (Ay) reaction components. The direction you initially draw these components is just an assumption. If you get a negative answer later, it simply means the actual direction is opposite to what you assumed.
2. Apply the Equilibrium Equations
Now we apply the three equations of equilibrium. Choose your coordinate system (usually x-axis is horizontal, and y-axis is vertical).
∑Fx = 0: Sum all the forces acting in the horizontal direction and set them equal to zero. This will often help you solve for Ax.
∑Fy = 0: Sum all the forces acting in the vertical direction and set them equal to zero. This will involve Ay and other vertical forces acting on the structure.
∑M = 0: Choose a point to take moments about. The point should be chosen strategically to eliminate unknown forces from the equation. Often, choosing the pin support (point A) or another support point is a good idea because the reactions at that point will not contribute to the moment equation (since the distance from the point to the force is zero).
3. Solve for Ax and Ay
Using the equations from step 2, solve for the unknown reactions Ax and Ay. You may need to solve a system of equations.
Remember, a negative sign indicates that the direction you initially assumed for the reaction is incorrect. Simply flip the direction of the arrow in your FBD and use the positive value for further calculations.
4. Calculate the Magnitude of the Reaction
The magnitude of the reaction at pin A (let's call it Ra) is the resultant of the horizontal and vertical components (Ax and Ay). We use the Pythagorean theorem to find the magnitude:
Ra = √(Ax² + Ay²)
This gives you the total force acting at the pin support A. It's the "size" or strength of the reaction force.
5. Find the Direction of the Reaction
You might also want to find the direction of the reaction force. This is the angle that the resultant force Ra makes with the horizontal axis.
We can use trigonometry to find the angle (let's call it θ):
θ = arctan(Ay / Ax)
This angle tells you the direction in which the reaction force is acting. Note that you need to consider the signs of Ax and Ay to determine the correct quadrant for the angle.
Example
Imagine a simple beam supported by a pin at point A and a roller at point B. A vertical load (F) is applied at the midpoint of the beam.
1. FBD: Draw the beam with the vertical load F acting downwards. Replace the pin at A with reactions Ax and Ay. Replace the roller at B with a vertical reaction By.
2. Equilibrium Equations: Assuming the beam is horizontal and length is 'L',
- ∑Fx = 0: Ax = 0 (since there are no other horizontal forces)
- ∑Fy = 0: Ay + By - F = 0
- ∑M_A = 0: (By * L) - (F * L/2) = 0 (Taking moments about point A)
3. Solve: From the moment equation, we get By = F/2. Substituting in the vertical force equation, we get Ay = F/2.
4. Magnitude: Ra = √(Ax² + Ay²) = √((0)² + (F/2)²) = F/2
5. Direction: θ = arctan(Ay / Ax) = arctan(F/2 / 0). Since Ax =0, the angle is 90 degrees (vertical).
So, the magnitude of the reaction at pin A is F/2, and it acts vertically upwards.
Important Considerations
Always double-check your work! Make sure your units are consistent and that your FBD is accurate.
The complexity of the problem can increase with more complex loading conditions or geometries. However, the fundamental principles remain the same.
Practice is key! The more problems you solve, the better you'll understand the concepts and the quicker you'll become at solving them.
Understanding these concepts is crucial for anyone studying engineering or physics. It allows you to analyze structures and ensure they can withstand the loads applied to them, ensuring safety and stability.