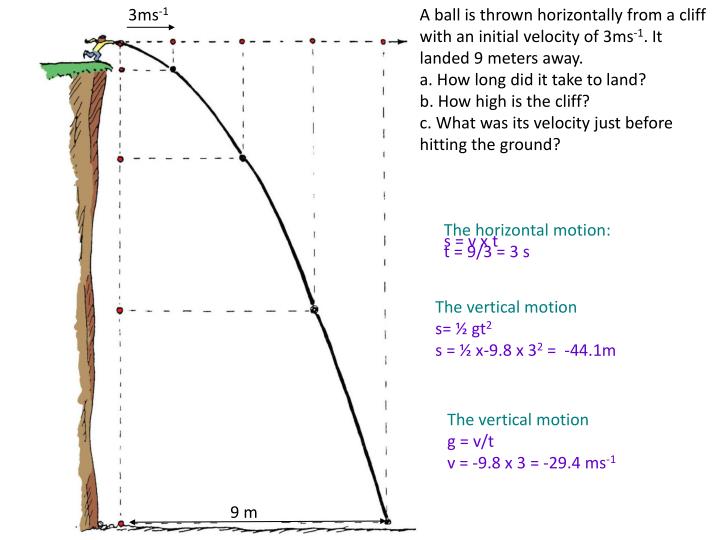
Let's explore what happens when something is thrown horizontally off a cliff. It's a classic physics problem. We'll break it down step by step. You'll see it's easier than it seems.
Key Concepts
Before we dive into the details, we need to understand some basic ideas. These ideas will help us understand the motion of the object. Understanding the terms makes everything easier.
Projectile Motion
Projectile motion is the motion of an object thrown into the air. Gravity is the only force acting on it. Air resistance is usually ignored. Imagine a basketball being thrown toward the hoop.
Horizontal Motion
Horizontal motion refers to movement in the left-right direction. If we ignore air resistance, the horizontal velocity is constant. This means it doesn't speed up or slow down.
Vertical Motion
Vertical motion refers to movement in the up-down direction. Gravity causes the object to accelerate downwards. The object's vertical speed increases over time.
Velocity
Velocity is the speed of an object in a specific direction. It's different from speed alone. Velocity also tells us which way the object is moving.
Acceleration
Acceleration is the rate at which velocity changes. A positive acceleration means the object is speeding up. A negative acceleration means the object is slowing down.
Gravity
Gravity is the force that pulls objects towards the Earth. On Earth, the acceleration due to gravity is approximately 9.8 m/s². This value is often represented as 'g'.
The Scenario: Object Thrown Horizontally
Imagine someone standing on the edge of a cliff. They throw a ball straight out, horizontally. The ball starts moving forward, but also starts falling down.
The ball's motion is a combination of two independent motions: horizontal and vertical. Let's look at them separately. Understanding both is key to solving the problem.
Horizontal Motion in Detail
Since we are ignoring air resistance, there's no force affecting the horizontal motion. The ball keeps moving forward at the same speed it was thrown. Think of a puck sliding on perfectly frictionless ice; it would keep going at the same speed.
If the initial horizontal velocity is 'v₀', the horizontal velocity at any time 't' will remain 'v₀'. The horizontal distance 'x' traveled after time 't' is given by: x = v₀ * t. This is a simple formula that only involves multiplying the initial velocity by time.
Vertical Motion in Detail
At the moment the ball is thrown, its initial vertical velocity is zero. Gravity starts pulling the ball down. The ball accelerates downwards at 'g' (9.8 m/s²). This is just like dropping the ball.
The vertical velocity 'v_y' at time 't' is given by: v_y = g * t. The vertical distance 'y' fallen after time 't' is given by: y = (1/2) * g * t². This means the further the object travels, the higher will the verical velocity become.
Analyzing the Trajectory
The trajectory is the path the object follows. In this case, it's a curve. This curve is called a parabola. It's the combination of constant horizontal motion and accelerating vertical motion. Picture the curved path of the ball as it flies through the air.
To determine the time it takes for the object to hit the ground, we only need to consider the vertical motion. The height of the cliff ('h') and the acceleration due to gravity ('g') are used. We use this formula: t = √(2h/g). This assumes the object is starting with zero veritcal velocity.
Once we know the time ('t'), we can find the horizontal distance ('x') the object travels before hitting the ground. Remember the formula: x = v₀ * t. The horizontal distance travelled is also called the *range*.
Putting It All Together: An Example
Let's say a ball is thrown horizontally at 10 m/s from a cliff that is 20 meters high. Let's find out how long it takes to hit the ground and how far it travels horizontally.
First, find the time it takes to hit the ground: t = √(2h/g) = √(2 * 20 / 9.8) ≈ √(4.08) ≈ 2.02 seconds. The ball will take about 2.02 seconds to reach the bottom of the cliff. No need to worry about the speed of the initial throw.
Next, find the horizontal distance: x = v₀ * t = 10 m/s * 2.02 s ≈ 20.2 meters. The ball will land approximately 20.2 meters away from the base of the cliff.
Important Considerations
We've made some simplifying assumptions. Real-world scenarios are more complicated. Air resistance affects both horizontal and vertical motion. This is generally hard to calcuate.
The object's shape and size also matter. A feather will be greatly affected by air resistance, but a rock won't be as much. Air resistance depends on the object's shape and speed.
The formulas we used are valid only when air resistance is negligible. However, this model gives you a good approximation for many real-world situations. For very complex calculations, you should utilize a computer to model the simulation.
In Summary
When an object is thrown horizontally off a cliff, its motion can be analyzed by considering horizontal and vertical motion independently. The horizontal motion is constant velocity. The vertical motion is accelerated motion due to gravity. The combination of these motions results in a parabolic trajectory. By understanding these concepts, you can predict the time of flight and the horizontal distance traveled. Remember to consider the assumptions we made!