Converting equations to slope-intercept form can be tricky. Let's explore how to rewrite 4x + 2y = 10 in this format. This conversion is a fundamental skill. It is important for understanding linear equations.
Understanding Slope-Intercept Form
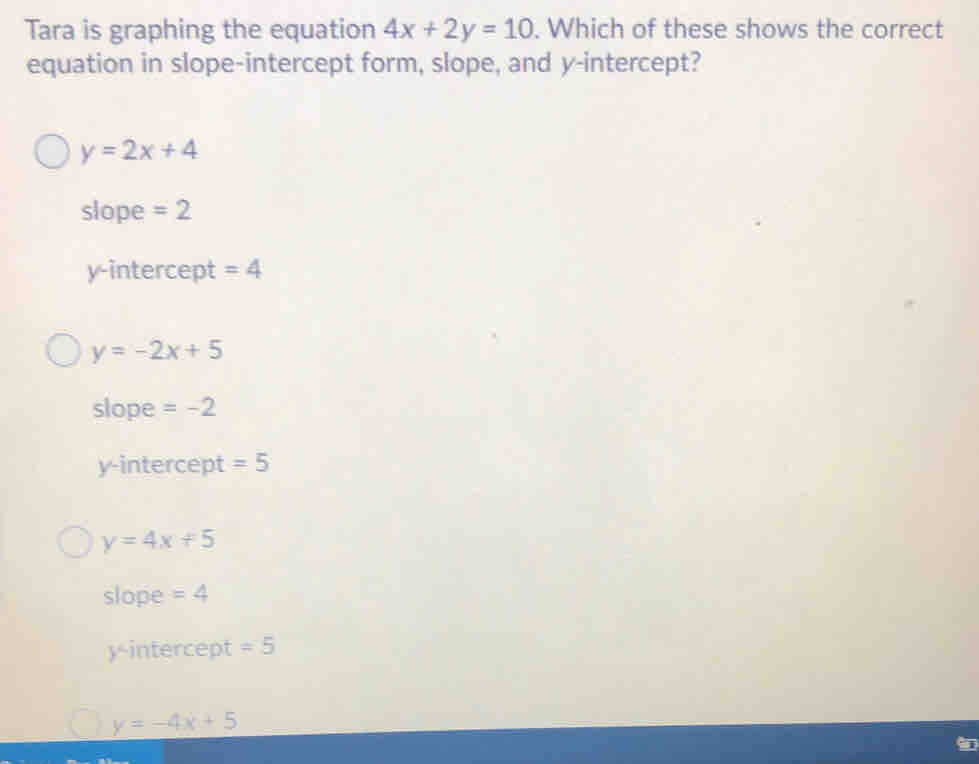
The slope-intercept form is written as y = mx + b. m represents the slope of the line. b represents the y-intercept. We need to manipulate the given equation. We must isolate 'y' on one side.
Step-by-Step Conversion
Start with the equation 4x + 2y = 10. Subtract 4x from both sides. This gives us 2y = -4x + 10.
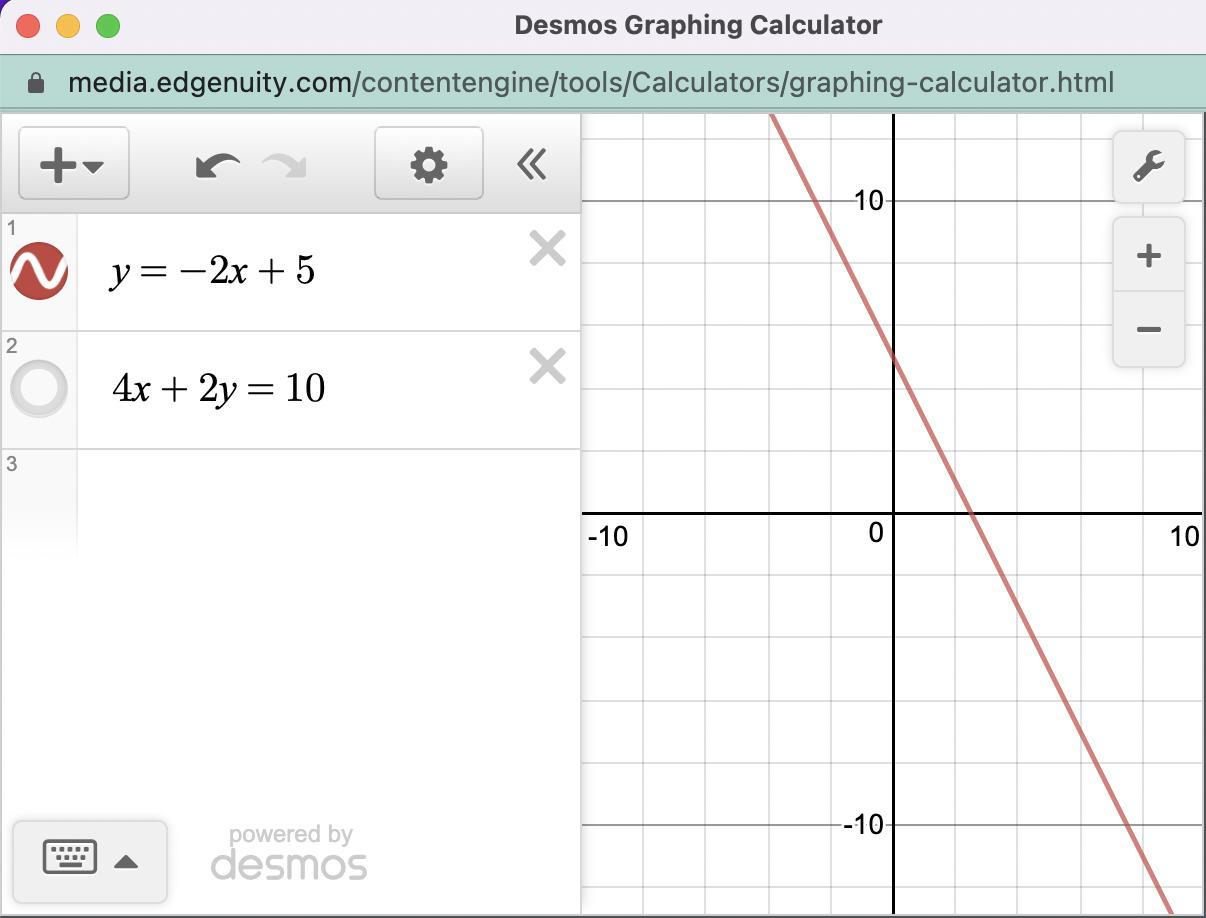
Now, divide both sides by 2. This isolates 'y'. The result is y = -2x + 5. The equation is now in slope-intercept form. We can identify the slope and y-intercept.
The slope (m) is -2. The y-intercept (b) is 5. Students can easily graph the line. They can also analyse its properties.
Teaching Strategies and Tips
Use visual aids to demonstrate the concept. Graphing the equation before and after conversion helps. Students visualize the transformation. This makes the concept more concrete.
Break down the steps clearly. Explain each operation performed. Emphasize maintaining equality on both sides. This prevents errors during the conversion process.
Provide plenty of practice problems. Start with simple equations. Gradually increase the complexity. Offer different types of linear equations for conversion. This reinforces understanding. It also builds confidence.
Encourage students to explain their reasoning. They can verbalize the steps they take. This helps identify any misunderstandings. It promotes deeper learning.
Addressing Common Misconceptions
A common error is incorrect sign manipulation. For example, failing to distribute a negative sign. Remind students to pay close attention to signs. Emphasize the rules of algebra. This is essential for accurate conversions.
Another misconception is confusing the slope and y-intercept. Reinforce the meaning of each component. Provide examples that highlight their roles. Use graphs to illustrate the difference.
Students may forget to divide all terms by the coefficient of 'y'. Stress the importance of dividing every term on both sides. This maintains the equality of the equation. Review distributive property rules.
Making it Engaging
Use real-world examples to illustrate linear equations. Relate slope and y-intercept to relatable scenarios. For example, the cost of a taxi ride. It might have a fixed initial fee (y-intercept) plus a cost per mile (slope).
Incorporate interactive activities. Use online graphing tools. Allow students to manipulate equations and observe the changes in the graph. This provides immediate visual feedback.
Create a game or competition. Divide the class into teams. Challenge them to convert equations into slope-intercept form. Award points for accuracy and speed. This makes learning fun and competitive.
Use technology to enhance learning. There are many apps and websites that can help. These resources offer interactive lessons and practice problems. Some generate step-by-step solutions. This provides individualized support.
Example Problem Walkthrough
Let's work through another example. Consider the equation -2x + 3y = 6. Our goal is to isolate 'y'.
First, add 2x to both sides. This gives us 3y = 2x + 6. Remember to keep the equation balanced.
Next, divide both sides by 3. This isolates 'y'. The result is y = (2/3)x + 2. The equation is now in slope-intercept form.
The slope is 2/3. The y-intercept is 2. Encourage students to graph this equation. This will reinforce their understanding.
Further Practice and Extension Activities
Assign additional practice problems. Include equations with fractions and decimals. This challenges students to apply their skills. It also helps them master the conversion process.
Explore parallel and perpendicular lines. Discuss how their slopes are related. This expands students' understanding of linear equations. It connects slope-intercept form to other concepts.
Introduce standard form of a linear equation. Show students how to convert between standard form and slope-intercept form. This builds a deeper understanding. It provides more flexibility in problem-solving.
Consider incorporating real-world data analysis. Students can create scatter plots. They can find the line of best fit. This applies the concepts to real-world scenarios. It demonstrates the practical use of linear equations.
By using these strategies and resources, educators can help students master the conversion of linear equations into slope-intercept form. This prepares them for more advanced mathematical concepts. It ensures a strong foundation in algebra.