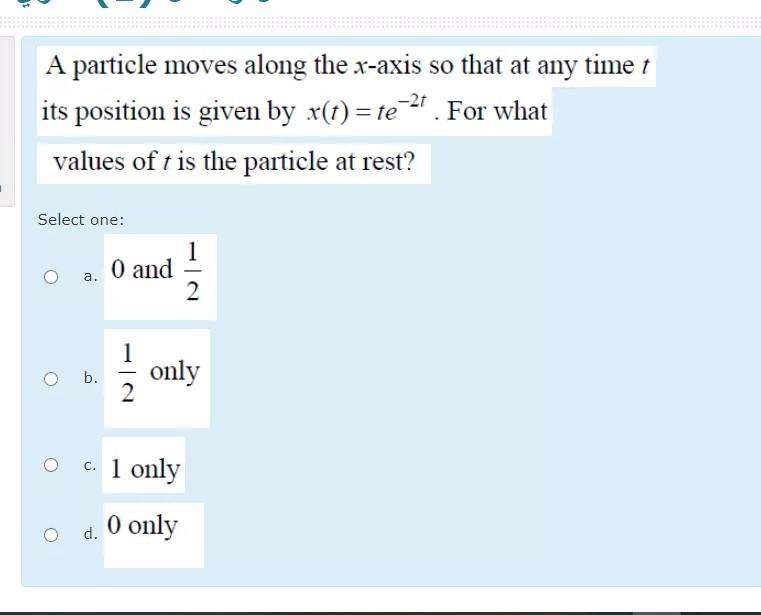
Hello! Let's talk about a particle moving along the x-axis. It sounds complicated, but we can break it down. We'll explore how its position changes over time. We will focus on the simple situation when time, denoted as T, is greater than or equal to zero. This means we're only concerned with what happens *after* a certain starting point.
What is a Particle?
First, what is a particle? In physics, a particle is simply an object we treat as a point. Its size and shape don't matter for the problem we are solving. Think of it like this: if you're tracking the movement of a car across a state, the car can be treated like a particle. You don’t really care about its length or width, just its overall location on the map.
Another example is a soccer ball. If you're only interested in how far it travels after being kicked, you might consider it a particle. You are focusing only on its center point and its trajectory. We are simplifying things to make the problem easier to solve, and this is very useful in physics.
The X-Axis
Next, the x-axis. This is just a horizontal line. It's like a number line that extends infinitely in both directions. We use it to represent the position of our particle. The position of our particle can be positive, negative, or zero.
Imagine a straight road. You can consider this the x-axis. A car moving along that road is our particle. Its position is determined by how far it is from a starting point that we designate as the origin (zero).
Time (T) Greater Than or Equal to Zero (0)
We are looking at the movement of our particle when T ≥ 0. T represents time. Time is usually measured in seconds, minutes, or hours. The "≥" symbol means "greater than or equal to".
So, T ≥ 0 means we start observing the particle at time zero. Everything before time zero doesn't concern us. It’s like pressing "start" on a stopwatch. We only care about the time that passes *after* we press start.
For instance, imagine you start watching a race. You only care about what happens from the moment the starting gun goes off (T=0) until the end of the race. The runner's training beforehand is irrelevant to our analysis of their speed during the race. This restriction is important for setting up the problem correctly.
Position as a Function of Time
Now, let's connect everything. The particle's position on the x-axis *depends* on time. We can describe this relationship with a function. We call this function x(T). x(T) tells you the position of the particle on the x-axis at any given time T.
For example, let's say x(T) = 2T. This means that at time T = 1 second, the particle is at position x = 2 * 1 = 2. At time T = 3 seconds, the particle is at position x = 2 * 3 = 6. The function tells us exactly where the particle is located at any point in time.
Let's say x(T) = T2 - T. This function is a little bit more complicated. At T = 0, x(0) = 02 - 0 = 0. At T = 1, x(1) = 12 - 1 = 0. At T = 2, x(2) = 22 - 2 = 2. This shows how the position of the particle changes with increasing time, given by the function x(T).
Velocity
The velocity of the particle is how quickly its position is changing. Mathematically, velocity is the derivative of the position function x(T) with respect to time T. We write velocity as v(T). If x(T) = 2T, then v(T) = 2. This means the particle is moving at a constant velocity of 2 units per unit time.
Consider the example where x(T) = T2. The velocity v(T) is the derivative of x(T) with respect to T, which is v(T) = 2T. Here, the velocity is not constant; it increases linearly with time. At T = 1, v(1) = 2, and at T = 3, v(3) = 6.
You can think of velocity as the speed and direction the particle is traveling. A positive velocity means the particle is moving to the right along the x-axis. A negative velocity means it's moving to the left. A velocity of zero means the particle is at rest.
Acceleration
Acceleration is how quickly the velocity of the particle is changing. Mathematically, acceleration is the derivative of the velocity function v(T) with respect to time T. We write acceleration as a(T). If v(T) = 2T, then a(T) = 2. This means the particle is accelerating at a constant rate of 2 units per unit time squared.
If velocity is constant (e.g., v(T) = 5), then the derivative (acceleration) is zero. If the velocity is decreasing over time, the acceleration will be negative. If the velocity is increasing over time, the acceleration will be positive.
Think of a car speeding up. That's positive acceleration. A car braking is negative acceleration (also called deceleration). Constant speed on a straight road has zero acceleration.
Putting It All Together
So, when we say "For T ≥ 0 a particle moves along the x-axis," we're talking about a situation where: * We are focused on the movement of a simplified object (a particle). * The particle is moving horizontally along a straight line (the x-axis). * We only care about the motion starting from time zero onwards. * The particle's position, velocity, and acceleration can all be described as functions of time: x(T), v(T), and a(T), respectively.
We use functions to describe how the position, velocity, and acceleration of the particle change over time. The position function x(T) gives the particle's location at any given time. The velocity function v(T) describes how fast the particle is moving and in what direction. The acceleration function a(T) tells us how quickly the velocity is changing.
Remember, we can use calculus (derivatives) to find the relationships between these functions. v(T) is the derivative of x(T), and a(T) is the derivative of v(T). Knowing the initial position and velocity, along with the acceleration, allows us to fully describe the particle's motion for all T ≥ 0.
An Example
Let’s consider a rocket launching vertically and simplifying to motion along the x-axis. Suppose the rocket's position is given by the function x(T) = 0.5T2. This indicates that the rocket's initial position is zero and its acceleration is constant. Then:
- The rocket's velocity, v(T), is the derivative of x(T), which is v(T) = T.
- The rocket's acceleration, a(T), is the derivative of v(T), which is a(T) = 1.
This means that the rocket starts at rest, and its velocity increases linearly with time. This also demonstrates an example of analyzing motion along one dimension.
Hopefully, this explanation has clarified what it means for a particle to move along the x-axis for T ≥ 0. Understanding these basic concepts is crucial for tackling more advanced topics in physics and engineering. Good luck with your studies!